体積(たいせき、英: volume)とは3次元空間において、その空間の領域の大きさを示す量(物理量)である。和語では嵩(かさ)という。
定義
上記の通り、三次元の構造(モノなど)の空間的な大きさの程度を示す量が体積であるが、厳密さが求められる数学においては、体積の定義の説明は複雑である。以下にその概略を示す(難解であれば、#体積の算出法へ読み進んでさしつかえない)。
体積は、3次元空間内の部分集合(すなわち三次元の図形)に対して規定することができる。この三次元図形は、定義関数によって指定(空間上の位置や形を決定)することができる。体積とは、この定義関数を3次元座標系の全体にわたって積分して得られる値である。たとえば、ユークリッド空間で直交座標系における定義関数f(x,y,z)を使うと、この関数で表現される三次元図形の体積は三重積分を用いて次のように表される。
この定義から、0次元の概念である点や、1次元の概念の線、2次元の面といった次元が3未満の図形の「体積」については、それぞれこの積分の値は0となる。
参考までに、体積のより広い概念として測度がある。
体積の公式
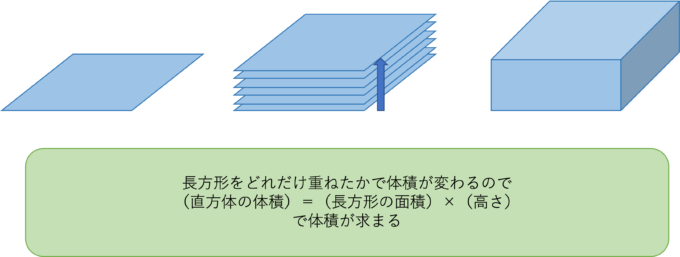
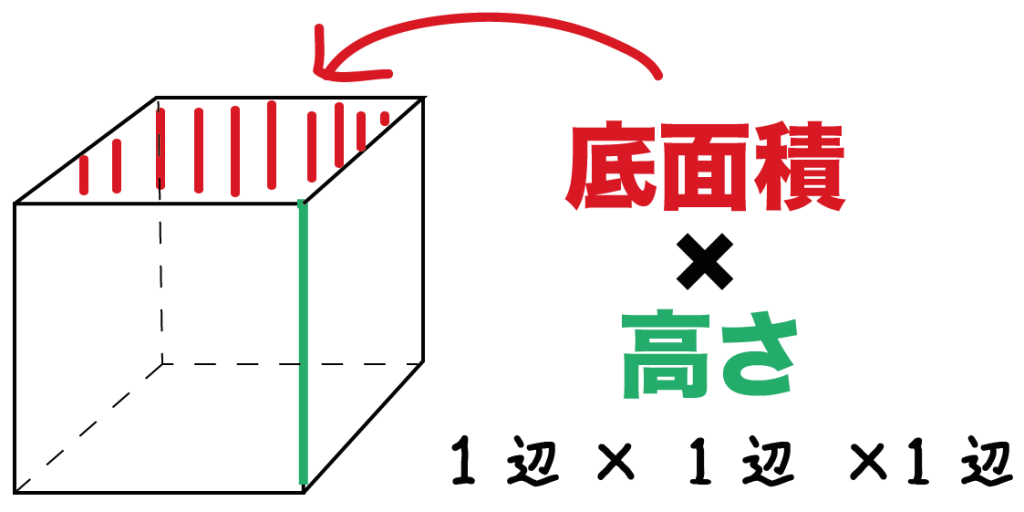
かいつまんでいえば体積とは、各片の長さがa, b, cの直方体に対して、積abcを計算したものである。これはもちろん上記の定義に則った結果である。基本的な三次元図形に対しては、上記の定義は簡単な計算式で表現することができる。以下にそれらの体積の計算法(公式)をいくつか示す。なお、式中のπ は円周率 (3.14…)である。
体積の単位
体積は、物理量としては「長さの3乗」の次元を有している。体積を計算する際に、長さの単位で表現される数値を(公式などで)計算するが、その長さの単位の3乗が一般に体積の単位となる。たとえば、mmであればmm3、kmであればkm3である。
国際単位系では、体積の単位は立方メートル (m3)を使用する。この単位は漢字で表記して立米(りゅうべい)と呼ばれることもある。また、立方センチメートル (cm3; ccやmLと同義)や、リットル (1,000 cm3 = L)も体積の単位として実用上よく用いられている。
尺貫法における体積の単位は、石・斗・升・合・才などがある。
体積の計測
化学分析では体積計が用いられる。特にガラス製のメスフラスコついては国際標準化機構 (ISO)にて詳細な構造や使用方法などの規格が定められている。
体積の計測にはメスフラスコ(全量フラスコ)のほか、ホールピペット(全量ピペット)やメスピペット、ビュレット、メスシリンダーがある。メスフラスコのように、容器の全量の目盛まで液体を入れたときに目盛り等の表記値が体積を表す受用の器具(英: To Contain (TC)、独: Einguss (E)で表記)、および、ピペットやビュレットのように、固有の排出時間内に排出先端より出た液の量を体積として表す出用の器具(同じくTo Deliver (TD)やAusguss (A)の表記)に、これらは分類される。
体積と容積
容積(ようせき)あるいは容量(ようりょう)は、ある容器の収納容量を考えたとき、その中に入り得る物体・物質の体積のことを指す。物理量としては、容積は体積と同じように算出可能であり、容積の単位は一般に体積と同じものを使用する。日本では、計量単位を定めている計量法体系において、「容積」の語が用いられることはなく、すべて「体積」あるいは「内容体積」と表記されている。食品表示基準においても、食品の内容量の表示規制として、「容積」ではなく「体積」あるいは「内容体積」が用いられている。
脚注
注釈
出典
関連項目
- 長さ
- 面積 - 表面積
- 体積の比較
- 調理用計量器
- 3D
- 体積形式