一般角

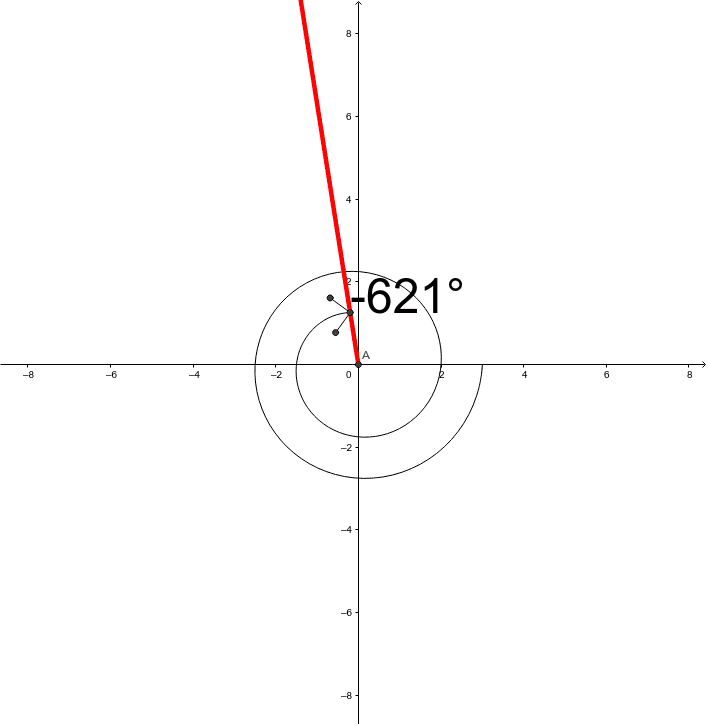
一般角（いっぱんかく、英語: general angle）とは、任意の角度を表す概念であり、特定の範囲に限定されない角度のことを指す。

概要

通常、三角法や幾何学において角度を考える際には、${\displaystyle 0^{\circ }}$から${\displaystyle 360^{\circ }}$までの範囲や、ラジアンで表現する場合は${\displaystyle 0^{\circ }}$から${\displaystyle 2\pi }$までの範囲で考えることが多い。

しかし、一般角はこのような特定の範囲に限定されず、例えば負の角度や${\displaystyle 360^{\circ }}$を超える角度も含まれる。

角に正負のみを与えたものは有向角と呼ばれる。

定義

一般角は以下のように定義される：

• 角度${\displaystyle \theta }$に${\displaystyle 360^{\circ }}$（または${\displaystyle 2\pi \,{\text{rad}}}$）を整数倍したものを足したり引いたりしたもの。
• すなわち、${\displaystyle \theta }$が一般角である場合、${\displaystyle \theta 360^{\circ }\times n}$または${\displaystyle \theta 2\pi \times n}$（${\displaystyle n\in \mathbb {Z} }$）も一般角である。

このようにして、一般角の概念を用いることで、複数回転や逆方向の回転など、さまざまな角度の状況を包括的に扱うことができる。

動径を用いて次の様にも定義される。

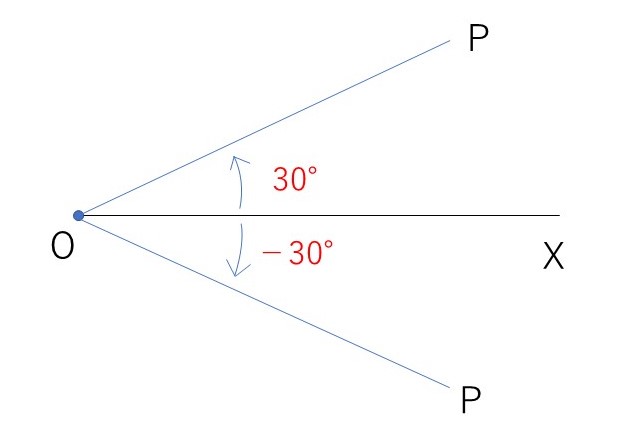
• 半直線OX（始線）をOを中心として回転させた半直線をORとする。OXとORの成す角を回転量と回転の向きで表したものを一般角と言う。

性質

三角関数

一般角と三角関数には深い関係がある。例えば以下の様な関係式が成立する。

極形式

角度を一般角に拡張した場合、極座標では点と点を表す実数の組が一対一で表せなくなる。

関連項目

• 符号付距離
• 符号付面積

出典

外部リンク

• 一般角-GeoGebra教材